Thermodynamics of the Climate System - The Diagnostic Tool TheDiaTo v1.0#
Overview#
The tool allows to compute TOA, atmospheric and surface energy budgets, latent energy and water mass budgets, meridional heat transports, the Lorenz Energy Cycle (LEC), the material entropy production with the direct and indirect method.
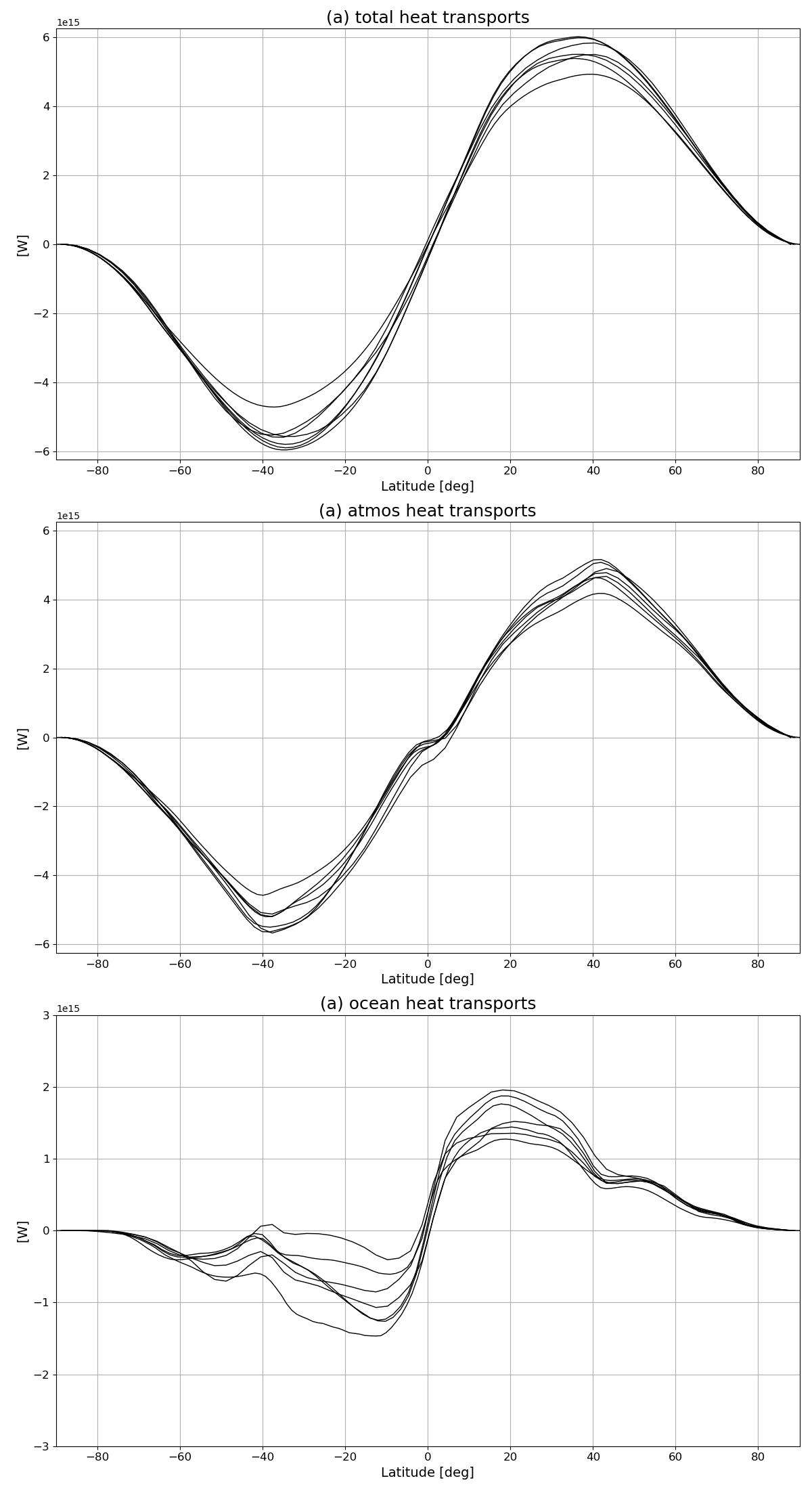
The energy budgets are computed from monthly mean radiative and heat fluxes at the TOA and at the surface (cfr. Wild et al., 2013). The meridional heat transports are obtained from the latitudinal integration of the zonal mean energy budgets. When a land-sea mask is provided, results are also available for land and oceans, separately.
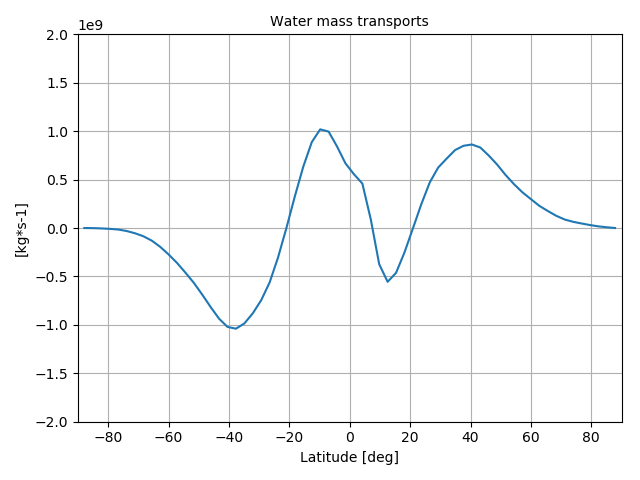
The water mass budget is obtained from monthly mean latent heat fluxes (for evaporation), total and snowfall precipitation (cfr. Liepert et al., 2012). The latent energy budget is obtained multiplying each component of the water mass budget by the respective latent heat constant. When a land-sea mask is provided, results are also available for land and oceans, separately.
The LEC is computed from 3D fields of daily mean velocity and temperature fields in the troposphere over pressure levels. The analysis is carried on in spectral fields, converting lonlat grids in Fourier coefficients. The components of the LEC are computed as in Ulbrich and Speth, 1991. In order to account for possible gaps in pressure levels, the daily fields of 2D near-surface temperature and horizontal velocities are needed. These are required to perform a vertical interpolation, substituting data in pressure levels where surface pressure is lower than the respective level and fields are not stored as an output of the analysed model.
The material entropy production is computed by using the indirect or the direct method (or both). The former method relies on the convergence of radiative heat in the atmosphere (cfr. Lucarini et al., 2011; Pascale et al., 2011), the latter on all viscous and non-viscous dissipative processes occurring in the atmosphere (namely the sensible heat fluxes, the hydrological cycle with its components and the kinetic energy dissipation).
For a comprehensive report on the methods used and some descriptive results, please refer to Lembo et al., 2019.
In order to account for possible gaps in pressure levels, the daily fields of 2D near-surface temperature and horizontal velocities.’
Available recipes and diagnostics#
Recipes are stored in recipes/
recipe_thermodyn_diagtool.yml
Diagnostics are stored in diag_scripts/thermodyn_diagtool/
thermodyn_diagnostics.py: the main script, handling input files, calling computation and plotting scricpts;
computations.py: a module containing all the main computations that are carried out by the program;
fluxogram.py: a module for the retrieval of the block diagrams displaying the reservoirs and conversion terms of the LEC
fourier_coefficients.py: a module for the computation of the Fourier coefficients from the lonlat input grid
lorenz_cycle.py: a module for the computation of the LEC components in Fourier coefficients
mkthe.py: a module for the computation of indirect variables obtained from the input fields, such as LCL height, boundary layer top height and temperature, potential temperature
plot_script.py: a module for the computation of maps, scatter plots, time series and meridional sections of some derived quantities for each model in the ensemble. The meridional heat and water mass transports are also computed here, as well as the peak magnitudes and locations;
provenance_meta.py: a module for collecting metadata and writing them to produced outputs;
User settings#
Besides the datasets, to be set according to usual ESMValTool convention, the user can set the following optional variables in the recipe_Thermodyn_diagtool.yml:
wat: if set to ‘true’, computations are performed of the water mass and latent energy budgets and transports
lsm: if set to true, the computations of the energy budgets, meridional energy transports, water mass and latent energy budgets and transports are performed separately over land and oceans
lec: if set to ‘true’, computation of the LEC are performed
entr: if set to ‘true’, computations of the material entropy production are performed
met (1, 2 or 3): the computation of the material entropy production must be performed with the indirect method (1), the direct method (2), or both methods. If 2 or 3 options are chosen, the intensity of the LEC is needed for the entropy production related to the kinetic energy dissipation. If lec is set to ‘false’, a default value is provided.
These options apply to all models provided for the multi-model ensemble computations
Variables#
Default variables needed for computation of energy budgets and transports:
hfls (atmos, monthly mean, time latitude longitude)
hfss (atmos, monthly mean, time latitude longitude)
rlds (atmos, monthly mean, time latitude longitude)
rlus (atmos, monthly mean, time latitude longitude)
rlut (atmos, monthly mean, time latitude longitude)
rsds (atmos, monthly mean, time latitude longitude)
rsdt (atmos, monthly mean, time latitude longitude)
rsus (atmos, monthly mean, time latitude longitude)
rsut (atmos, monthly mean, time latitude longitude)
Additional variables needed for water mass and latent energy computation (optional, with ‘wat’ set to ‘true’):
pr (atmos, monthly mean, time latitude longitude)
prsn (atmos, monthly mean, time latitude longitude)
Additional variable needed for LEC computations (optional, with ‘lec’ set to ‘true’):
ta (atmos, daily mean, time plev latitude longitude)
tas (atmos, daily mean, time latitude longitude)
ua (atmos, daily mean, time plev latitude longitude)
uas (atmos, daily mean, time latitude longitude)
va (atmos, daily mean, time plev latitude longitude)
vas (atmos, daily mean, time latitude longitude)
wap (atmos, daily mean, time plev latitude longitude)
Additional variables needed for material entropy production computations with direct method (optional, with ‘entr’ set to ‘true’ and ‘mep’ to ‘2’ or ‘3’):
hus (atmos, monthly mean, time plev latitude longitude)
pr (atmos, monthly mean, time latitude longitude)
prsn (atmos, monthly mean, time latitude longitude)
ps (atmos, monthly mean, time latitude longitude)
ts (atmos, monthly mean, time latitude longitude)
Additional variables needed for material entropy production computations with indirect method (optional, with ‘entr’ set to ‘true’ and ‘mep’ to ‘1’ or ‘3’):
tas (atmos, daily mean, time latitude longitude)
uas (atmos, daily mean, time latitude longitude)
vas (atmos, daily mean, time latitude longitude)
Depending on the user’s options, variables listed above must be provided. All other variables shall be commented in the recipe file.
References#
Lembo V, Lunkeit F, Lucarini V (2019) A new diagnostic tool for diagnosing water, energy and entropy budgets in climate models. Geophys Mod Dev Disc. doi:10.5194/gmd-12-3805-2019
Liepert BG, Previdi M (2012) Inter-model variability and biases of the global water cycle in CMIP3 coupled climate models. Environ Res Lett 7:014006. doi: 10.1088/1748-9326/7/1/014006
Lorenz EN (1955) Available Potential Energy and the Maintenance of the General Circulation. Tellus 7:157–167. doi: 10.1111/j.2153-3490.1955.tb01148.x
Lucarini V, Fraedrich K, Ragone F (2010) New Results on the Thermodynamical Properties of the Climate System. J Atmo 68:. doi: 10.1175/2011JAS3713.1
Lucarini V, Blender R, Herbert C, et al (2014) Reviews of Geophysics Mathematical and physical ideas for climate science. doi: 10.1002/2013RG000446
Pascale S, Gregory JM, Ambaum M, Tailleux R (2011) Climate entropy budget of the HadCM3 atmosphere–ocean general circulation model and of FAMOUS, its low-resolution version. Clim Dyn 36:1189–1206. doi: 10.1007/s00382-009-0718-1
Ulbrich U, Speth P (1991) The global energy cycle of stationary and transient atmospheric waves: Results from ECMWF analyses. Meteorol Atmos Phys 45:125–138. doi: 10.1007/BF01029650
Wild M, Folini D, Schär C, et al (2013) The global energy balance from a surface perspective. Clim Dyn 40:3107–3134. doi: 10.1007/s00382-012-1569-8
Example plots#